Yet a simple question in appearance, but whose response can not be invented : what is an image ?

Depending on the context in which it takes place, this question accepts multiple answers to be very different. In this chapter we will address both the theoretical point of view and the technical point of view. We learn, therefore, to represent images in gray levels in mathematics, as well as in the memory of your computer, and we will discover how these can be handled with OpenCV.

Ah ! And then as I promised in the previous chapter, you’ll also meet Lena, our lovely new assistant and guinea pig.

Formal representation

A ” function of light intensities “

Whether it is this that captures the retina at the back of the eye or the photosensitive sensor of a webcam, an image, is nothing other than the projection of light rays from the outside world on a plane.

If it does not belong to us in this chapter to study the concepts of optical or projective geometry that underlie this phenomenon (which will come in a much more advanced this course), this definition has its importance for understanding the way in which images are modelled in mathematics.

In a first step, we will make the assumption that the rays of light that strikes the plane of the image are characterized by their intensity only. This means that on our plan, we will provide a reference in good cartesian that we are, we associate to each pair of coordinates, $\((x,y)\)$ a value $\(I(x,y)\)$ that we will call a gray level : the higher the point is bright, the more the value of the gray level is high. Therefore, one may consider that an image is a function defined like this :

$\(\begin{matrix}I\;: & \mathbb{R}^2 & \rightarrow & \mathbb{R} \\ & (x,y) & \mapsto & I(x,y)\end{matrix}\)$

This is considerably convenient ! With this definition, we will be able to represent the images in an abstract way, and to make image processing in the language of mathematics, the most precise and least ambiguous.

But wait a little…

Unless we live you and me in a perfectly mathematical, this definition, as precise and rigorous as it is, remains still very limited. Can you guess why ?

Bingo !
As simple the mathematical definition of an image as it is, we are absolutely unable to get the “formulas” of images of the real world. In fact, from a mathematical point of view, when we look at an image, what we see is sort of the curve (or rather, here, the ” surface “) of a function, that is to say, the values that it takes according to $\(x\)$ and $\(y\)$.

This means that to study the images of the real world, we’re going to have to observe, not functions as such, but the result, or rather, to use the mathematical term exact, the imagesof these functions…

A ” matrix of pixels “

Even if we can’t find a beautiful formula for each photo in the real world, and that we must be content to observe light intensities on a plane, do not give up mathematics too soon, but take the opportunity to make a few adjustments to fit the images in the memory of our computers.

First of all, let’s get rid of the infinitely small !

In fact, it is neither practical, nor feasible to observe the entire surface in the plane $\(\mathbb{R}^2\)$ for an image. Intuitively, this would mean that we could know the light intensity at the point $\((3,5)\)$ as well as that at the point $\((3.0029, 4.9987)\)$, and even that we could even capture the infinity of the light intensities on the segment connecting these two points, which is not possible even in the real world, saw that the sensors of the cameras, just as our retinas are composed of a number of finished cells…

Thus, our observations on the image plane will be on points of whole coordinates, which means that we can store all the levels of grey that it captures in a nice table like the following :

$\(\begin{pmatrix}I(0,0) & I(1,0) & I(2,0) & \dots & I(w-1,0) \\I(0,1) & I(1,1) & I(2,1) & \dots & I(w-1,1) \\I(0,2) & I(1,2) & I(2,2) & \dots & I(w-1,2) \\\vdots & \vdots & \vdots & \ddots & \vdots \\I(0,h-1) & I(1,h-1) & I(2,h-1) & \dots & I(w-1,h-1)\end{pmatrix},\)$

where $\(w\)$ is the breadth (width) of the image and $\(h\)$ its height (height). In mathematics, such two-dimensional arrays are called matrices. We can therefore formulate our new definition, one that we will keep throughout this course : a digital image is a matrix of pixels.

A pixel, it is literally “an element of an image” : the word pixel comes from the English “picture element“. In a first step, we will simply consider that a pixel is a gray level, but you will see in the next chapter that this is not always the case.

Some considerations on matrices

Given that you are not supposed to have already handled matrices in math, here are a few general considerations on the matrices.

If $\(M\)$ is a matrix with $\(n\)$ rows and $\(p\)$ columns :

• It is said that $\(M\)$ is a matrix $\(n\times p\)$ and can be noted $\(M_{n\times p}\)$.

• Its elements, which are noted $\(m_{i,j}\)$ for $\(0 \leq i < n\)$ and $\(0 \leq j < p\)$ are called scalars.

• Attention to the indexing. In the notation $\(m_{i,j}\)$, we give first the row number $\(i\)$then the column number $\(j\)$. This means that in the picture we have above, the gray level $\(I(x,y)\)$ is carried by the pixel $\(m_{y,x}\)$.

• His ” origin “, the scalar $\(m_{0,0}\)$, is conventionally in the top left.

Example

In order to properly show you the link between an image and a matrix, take the small piece of the following image :

Here it is enlarged 20 times :

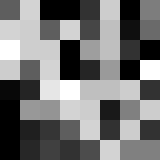
And now here is the corresponding matrix :

$\(\begin{pmatrix}94 & 211 & 0 & 0 & 50 & 205 & 0 & 125 \\211 & 206 & 94 & 211 & 70 & 191 & 15 & 106 \\255 & 206 & 206 & 0 & 158 & 191 & 50 & 0 \\205 & 94 & 211 & 0 & 37 & 154 & 0 & 255 \\8 & 36 & 230 & 255 & 191 & 191 & 205 & 50 \\0 & 152 & 148 & 211 & 205 & 25 & 128 & 205 \\0 & 31 & 53 & 94 & 211 & 49 & 205 & 50 \\0 & 39 & 64 & 50 & 76 & 211 & 128 & 128 \\\end{pmatrix}\)$

As you can see, the white pixels correspond to the gray level 255, while black pixels correspond to the level 0. It is said that the light intensity is sampled on 256 values. We will return to this idea later.

I think this should be enough math for the time being. How would you like to come to practice and see how it goes in the memory of your computer ?

The eyesweb project has many articles similar to this one. Check them out

Yes good, in fact, I won’t leave you the choice. 
Go, later !

The structure IplImage

Now that we’ve established that digital images are matrices of pixels, let us consider for a few moments on the structureIplImagein OpenCV.

Data representation

What type are the data of the image within aIplImage ?
Reflex : a quick look at the documentation will give you the answer. Here’s what you should find :

typedef struct _IplImage
{
  // ...
  char *imageData;
  // ...
} 
IplImage;

Yeah !"dessine-moi un mouton"… Hum, not ! >_
Typecharis used here because it represents exactly one byte in memory. It is thus necessary to read the data of the image are contained in the most natural way of the world in a byte array, even if the pixels do not necessarily on a byte (we will return to this point in a few moments).

Thus, either in mathematics or in the RAM of your machine, I will say it once again : an image is neither more nor less than a table.

Well ! But this does not tell us yet in what order is stored this table in memory. For this, we will need to follow a little more in detail the structureIplImage :

typedef struct _IplImage
{
  // ...
  int  width;      // nb de colonnes de la matrice
  int  height;     // nb de lignes de la matrice
  // ... 
  int  imageSize;  // taille totale des données en octets 
  char *imageData; // pointeur sur les données
  int  widthStep;  // largeur d'une ligne en octets
  // ...
}
IplImage;

Although this is not necessarily obvious at first (but I invite you to think about it as exercise), one can deduce from this bit of declaration that the images in OpenCV are stored in memory line by line. In English, it is called row-major order.

The following diagram shows you my poor talents as a draftsman, a gray level image with few pixels is outstanding, as well as how it will be stored in memory by OpenCV :

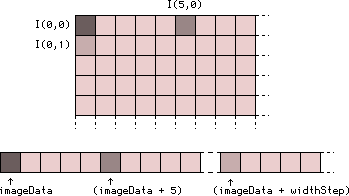
To understand this pattern, here are a few examples to remind you of your deep love for pointer arithmetic. Ifimgis aIplImage*containing a grayscale image whose pixels arechar, then :

• img->imageDatais the address of the pixel coordinates $\((0,0)\)$, the first pixel of the image ;

• (img->imageData + 7)is the address of the pixel coordinates $\((7,0)\)$, the eighth pixel of the first line ;

• (img->imageData + img->widthStep)is the address of the pixel coordinates $\((0,1)\)$, the first pixel of the second line ;

• (img->imageData + (3 * img->widthStep) + 12)is the address of the pixel coordinates $\((12,3)\)$, the thirteenth pixel of the fourth line ;

• (img->imageData + img->imageSize)is the address of the byte located just after the last pixel of the image.

Well seen ! In the case of gray level images whose pixels arechar, it is very likely indeed that the fieldswidthandwidthStepare equal. That said, there are two major reasons why one cannot assume that this is the case.

The first reason is that OpenCV, internally, may decide that the lines of the image will not necessarily be contiguous in memory, but that they will be aligned on a byte accurate, so as to improve the performance. When this is the case, this alignment of a few bytes is added to the fieldwidthStepthen thatwidthwill always be exactly the number of columns of the image.

The second reason, more simple, is that the gray levels are not alwayschar, and this is what we’re going to see just now.

The “depth ” of the images

It is possible that you have already heard of” images of 8, 16, or 32 bits “. In this expression, the number of bits refers to the size of a pixel in memory. This is called the depth (depth) of the image.

If you again look at the mathematical definition that we formulated at the beginning of this chapter, you will see that there is nothing in what we have said, does not give us the type of gray levels, or even values that can take these light intensities. This is simply because you can use several different types to describe a level of grey, and it is the depth of the image that determines the type used.

In any rigour, the depth of an image describes the number of values on which the light intensity is sampled. For example, on an image in 8 bit grayscale (unsigned), the light intensity will be sampled on 256 values, with 0 for black and 255 for white, then that on a 16-bit image, the light intensity will take 65536 different values (0 for black and 65535 as white), which can be 256 times more precise than 8 bits, but takes twice more space in memory…

This depth, in OpenCV, is described by the fielddepthof the structureIplImage. This field contains a constant that is defined by OpenCV in the following form :

IPL_DEPTH_[Nombre de bits][Type].

The following table describes the correspondence between the types of pixels, their sizes, the sets of possible values, and the constants of depth in OpenCV :

“Don’T PANIC !” says the Guide.
In reality, we will work almost exclusively with images of depth8U, that is to say, with intensities between 0 and 255. You are absolutely not forced to learn this table by heart : now that you’ve seen, you know that he is here, and you can see the day when you will need it !

That said, I have the pleasure to announce you that we almost finished with the dissection of the structureIplImage. It remains for us more than a few utility functions to discover before making a small pause.

Some utility functions before the break

As you have probably noticed by reading the documentation, the structureIplImageis much larger than we have seen for the moment. In reality, many of the fields we will be not be useful before a good time, and those that we’ve seen are practically the only ones that you need to know in order to follow this course.

Now that the time to play with images that is fast approaching, let’s see how we create one of these structures. Once again (yes, I know, I ramble), the documentation is our best friend, and we provides the following function :

/**
 * Alloue une structure IplImage
 * arguments:
 * - size: la taille de l'image à allouer 
 * - depth: profondeur de l'image
 * - channels: nombre de canaux de l'image
 * retourne:
 * un pointeur sur l'IplImage allouée
 */
IplImage* cvCreateImage(CvSize size, int depth, int channels);

The structureCvSizeis no other than the association of two integers describing the width and height of the image. As to the number of channels, we will use that one for the moment, but will see the significance of this field in the next chapter.

Here’s an example where I create an image of width 640 and height 480, and the pixels will beunsigned char :

IplImage* img;
img = cvCreateImage (cvSize (640, 480), IPL_DEPTH_8U, 1);

Simple, no ?
Before you move on, I remind you, just the signature of the function to deallocate a structureIplImageas well as its data.

/**
 * Désalloue la mémoire occupée par une IplImage
 */
void cvReleaseImage(IplImage** image);

No difficulty here, if it is not, I remind you, that it is necessary to think well to move a pointer on pointer on IplImagethis function.

On these good words, the time has come for us to blow off a little !

Browse a image

Our test image

Before you begin to play with images, let me, by way of a break since the beginning of this chapter was rather dense, you present the image that we will use for most of our tests, Lena.

This image, as I’ve already said in the previous chapter, is the small square of 512×512 pixels, the most famous in the world of research and engineering in imaging, which is certainly worth the title of “mona lisa” computer vision “. Here is his story.

It all began in the laboratory SIPI) from the prestigious University of Southern California, in which were conducted the research that would eventually lead to the compression standards JPEG and MPEG, which we all know today.

By a beautiful day of the summer of 1973, three researchers from this laboratory were busy, in the emergency, in search of a example image that is new and sufficiently sympathetic to be published in the conference paper of one of their colleagues, regarding the latest results of his research in the field of image compression. It is then that a person walked into their office a magazine in the hands, magazine page central of which was the photo of a woman, named Lena.The decision was not long to take : our researchers pulled out the photograph of the said magazine, the numérisèrent with the means of the time, and retaillèrent the result to get the square image of 512×512 pixels that you have under the eyes.

The story could have stopped here, if it was only a score of years later, so that this image had become a standard by which the researchers could compare their compression algorithms, and distributed and pay by the IIPS, the magazine of the origin of the photo is manifesta, a relatively angry to see his property re-used without paying him his rights, which marked also the beginning of a noisy controversy within the scientific community. In fact, Lena Sjööblom is none other than the miss Playboy for the month of November 1972 !

Today, this photo is freely accessible and free of charge, and continues to be the most used to test image processing algorithms, not because of the enigmatic gaze of the girl, but rather because of the full range of texture thin, surfaces are relatively uniform, contours and details that make up its richness (… Well, probably also because it is pretty, though).

You can find the original image in TIFF format (so uncompressed) here. This is the one I recommend you use to test your algos of all kinds, rather than JPEG, since, in some cases, the JPEG compression will appear as unwanted artefacts in your results.

On this, the pause is complete.

Several different methods

In the remainder of this sub-section, we will encode, in many possible ways, a small program that opens an image in 8 bit grayscale, and reverse the pixels.

This means that the transformation that we are going to make will be the following function, where $\(\mathrm{dst}\)$ is the image of result and $\(\mathrm{src}\)$ the original image :

$\(\mathrm{dst}(x,y) = 255 – \mathrm{src} (x,y)\)$

Here is the expected result, in all cases, the photo of Lena :

To make our lives easier, we will simply write a functioninversethat takes in argument aIplImage*and reverse the image contained in place.

Here is the body of the program which we are going to work.

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <opencv/cv.h>
#include <opencv/highgui.h>

/**
 * Inverse une image "en place"
 */
void invert (IplImage* img)
{
  assert (img->depth == IPL_DEPTH_8U && img->nChannels == 1);
  // TODO 
}

/**
 * Ce programme prend deux arguments dont un optionnel:
 * IMAGE:     l'image à inverser
 * SAVE_PATH: (optionnel) l'image dans laquelle sauvegarder le résultat
 */
int main (int argc, char* argv[])
{
  IplImage* img = NULL; 
  const char* src_path = NULL;
  const char* dst_path = NULL;
  const char* window_title = "Inverse";

  if (argc < 2)
  {
    fprintf (stderr, "usage: %s IMAGE [SAVE_PATH]\n", argv[0]);
    return EXIT_FAILURE;
  }

  src_path = argv[1];

   // optionnel: sauvegarde du résultat 
   // si un second chemin est passé au programme
  if (argc > 2) 
    dst_path = argv[2];

  if (!(img = cvLoadImage (src_path, CV_LOAD_IMAGE_GRAYSCALE)))
  {
    fprintf (stderr, "couldn't open image file: %s\n", argv[1]);
    return EXIT_FAILURE;
  }

  invert (img);

  cvNamedWindow (window_title, CV_WINDOW_AUTOSIZE);
  cvShowImage   (window_title, img);
  cvWaitKey (0);
  cvDestroyAllWindows ();
  
  if (dst_path && !cvSaveImage (dst_path, img, NULL))
  {
    fprintf (stderr, "couldn't write image to file: %s\n", dst_path);
  }
  
  cvReleaseImage(&img);
  return EXIT_SUCCESS;
}

As you can see, I have taken care of me take care of all the cosmetic to your place (loading of the image and convert to grayscale, registration optional, display of the result…), so that we do not need to occupy us all than the functioninvert.

You’ll notice that I highlighted the line 12, because I use the function assert that you have perhaps not yet cross. This function simple takes a condition in argument and crashes the program if it is not met. This is a security that can detect right away if something is not working normally in your code. His other interest is that once you have finished testing your program in every sense, you can gain a little performance by disabling this feature (which will become “invisible” to the compiler), simply by using the constantNDEBUGat compile-time. You can find more information about it here.

In our code, this line makes sure that the image passed as an argument to the functioninvertis indeed a gray scale image of 8 bits.

The method is simple : the functions cvPtr*D

To reverse our image, there are not 36 possible ways : it is sufficient for us, for each pair of coordinates $\((x,y)\)$, to retrieve a pointer to the corresponding pixel, and to operate the change over. What we’re going to see until the end of this sub-part, three methods more and more low-level for it.

To retrieve a pointer to a given pixel of a grayscale image, we can use the function cvPtr2D, here is the signature :

/**
 * Récupérer un pointeur sur un élément donné d'un tableau.
 * arguments:
 * - arr: image (ou matrice) à parcourir
 * - idx0: numéro de ligne du pixel
 * - idx1: numéro de colonne du pixel
 * - type: paramètre optionnel de sortie, décrivant la profondeur
 *         du tableau
 * retourne:
 * un pointeur sur l'élément du tableau visé.
 */
uchar* cvPtr2D (const CvArr* arr, int idx0, int idx1, int* type);

Pay Attention to the order of the arguments : it must first pass to this function the row number of the pixel (i.e. the coordinate $\(y\)$) and then the column number (the y coordinate $\(x\)$). The optional parametertypedoes not interest us for the moment : you can leave itNULLmost of the time.

Here is an implementation of the functioninvertusing cvPtr2D to browse the image.

void invert (IplImage* img)
{
  int x,y;
  uchar *p;
  assert (img->depth == IPL_DEPTH_8U && img->nChannels == 1);

  for (y = 0; y < img->height; ++y)
  {
    for (x = 0; x < img->width; ++x)
    {
      // récupération d'un pointeur sur le pixel de coordonnées (x,y)
      p = cvPtr2D (img, y, x, NULL);
      *p = 255 - *p;
    }
  }
}

As you can see, the code is rather direct. What is interesting to note, is that the functioncvPtr2Dperforms exactly the little calculation about pointers that I showed you earlier. This can be demonstrated by instead using the functioncvPtr1D :

/**
 * Retourne un pointeur sur le pixel de coordonnée idx.
 */
uchar* cvPtr1D (const CvArr* arr, int idx, int* type);

This function performs the same operation as the previous, but considering this time that the array passed as an argument has only a single dimension. To use it, so we have to calculate the location of the pixel referred to ourselves, like this :

void invert (IplImage* img)
{
  int x,y;
  uchar *p;
  assert (img->depth == IPL_DEPTH_8U && img->nChannels == 1);

  for (y = 0; y < img->height; ++y)
  {
    for (x = 0; x < img->width; ++x)
    {
      // récupération d'un pointeur sur le pixel de coordonnées (x,y)
      p = cvPtr1D (img, y * img->widthStep + x, NULL);
      *p = 255 - *p;
    }
  }
}

The only line that changes in this code is the one highlighted. As you can see, the calculation of the index of the pixel gives exactly the above in this chapter.

The quick method : direct access to the pointer

The only drawback of the previous method to browse a picture, this is the index of the pixel is fully recalculated at each passage in the second loop. It should not be very complicated to find a more direct way to scan the entire image, without the need of a function to do this.

Here is the latest complete implementation of the functioninvertas we will see in this chapter :

void invert (IplImage* img)
{
  uchar *p, *line;
  assert (img->depth == IPL_DEPTH_8U && img->nChannels == 1);

  // parcours des lignes de l'image
  // on positionne le pointeur "line" sur le début de l'image
  // et on le fait avancer de la taille d'une ligne à chaque itération
  // jusqu'à tomber sur l'octet suivant le dernier pixel de l'image
  for (line = (uchar*) img->imageData; 
       line < (uchar*) img->imageData + img->imageSize; 
       line += img->widthStep)
  {
    // parcours de la ligne "line"
    // on positionne le pointeur p sur le début de la ligne
    // et on le fait avancer de la taille d'un pixel à chaque itération
    // jusqu'à tomber sur le dernier pixel de la ligne
    for (p = line; p < line + img->width; ++p)
    {
      *p = 255 - *p;
    }
  }
}

This code, though somewhat confusing at first if you do not have the habit of playing with pointers in this way, is not especially complicated (the comments are there to guide you). I advise you to unroll it slowly in your head until it is clear to you, because that is how we follow our matrices each time that we will need to make a ” full-scan “.

The method that kills

For the tougher of you, still, here is a final implementation of the functioninvert, very in the margin of this chapter, but I’ll let you analyse as an exercise in helping you to the documentation of the functioncvNot:

void invert (IplImage* img)
{
  cvNot (img, img);
}

Exercises

In order to return everything that we have seen so far, here’s a quick exercise fix.

Overlay of two images

Here are two photos of Lena very noisy :

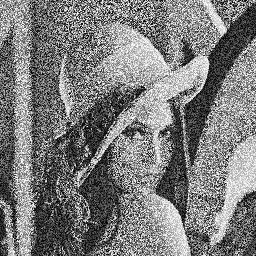
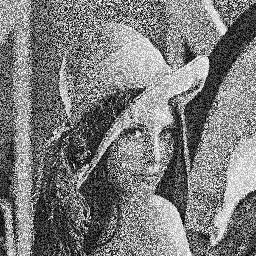
These two images may appear identical at first glance, but rather, they are entirely complementary. In fact, if you overlay, you will get the original image.

The aim of the exercise will be for you to create a program which will calculate the average of these two images, that is to say, the treatment that can be summarized by the following formula :

$\(\mathrm{dst(x,y)} = \dfrac{\mathrm{src1}(x,y) + \mathrm{src2}(x,y)}{2}\)$

You can check your program by just looking at if it correctly reconstructs the original image or not.

Read about the newest wireless technology news from eyesweb

Before you start to code

Before you put in the work, there is another consideration of a practical nature as we have to see together, especially if you are working under Windows. In this OS, the functioncvLoadImagehas the unfortunate tendency not to place the origin of the images in the right place. In fact, it happens that the images in Windows to be loaded with the origin at the bottom left, so that without attention, your picture of result risk of finding themselves the head down.

Here is a small function, thanks to which you will be able to solve this problem :

/**
 * Corrige l'origine de l'image si nécessaire
 */
void fix_origin (IplImage* img)
{
  if (img->origin == IPL_ORIGIN_BL)
  {
    cvConvertImage(img, img, CV_CVTIMG_FLIP);
    img->origin = IPL_ORIGIN_TL;
  }
}

On this, at work !

Solution(s)

Here is a possible solution to this exercise :

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <opencv/cv.h>
#include <opencv/highgui.h>

/**
 * Calcule la moyenne des images src1 et src2.
 * Stocke le résultat dans l'image dst.
 */
void superpose (const IplImage *src1, const IplImage *src2, IplImage* dst)
{
  int x, y;
  uchar *p_dst, *p_src1, *p_src2;

  assert (src1->width == src2->width);
  assert (src1->height == src2->height);

  for (y = 0; y < dst->height; ++y)
  {
    for (x = 0; x < dst->width; ++x)
    {
      p_src1 = cvPtr2D (src1, y, x, NULL);
      p_src2 = cvPtr2D (src2, y, x, NULL);
      p_dst  = cvPtr2D (dst , y, x, NULL);

      *p_dst  = *p_src1 / 2 + *p_src2 / 2;
    }
  }
}

/**
 * Corrige l'origine de l'image si nécessaire
 */
void fix_origin (IplImage* img)
{
  if (img->origin == IPL_ORIGIN_BL)
  {
    cvConvertImage(img, img, CV_CVTIMG_FLIP);
    img->origin = IPL_ORIGIN_TL;
  }
}

/**
 * Ce programme prend deux arguments : les deux images à superposer.
 */
int main (int argc, char* argv[])
{
  IplImage* src1 = NULL; 
  IplImage* src2 = NULL; 
  IplImage* dst  = NULL; 
  const char* src1_path = NULL;
  const char* src2_path = NULL;
  const char* window_title = "Superpose";

  if (argc < 3)
  {
    fprintf (stderr, "usage: %s SRC1 SRC2\n", argv[0]);
    return EXIT_FAILURE;
  }

  src1_path = argv[1];
  src2_path = argv[2];

  if (!(src1 = cvLoadImage (src1_path, CV_LOAD_IMAGE_GRAYSCALE)))
  {
    fprintf (stderr, "couldn't open image file: %s\n", src1_path);
    return EXIT_FAILURE;
  }

  if (!(src2 = cvLoadImage (src2_path, CV_LOAD_IMAGE_GRAYSCALE)))
  {
    fprintf (stderr, "couldn't open image file: %s\n", src2_path);
    return EXIT_FAILURE;
  }

  fix_origin (src1);
  fix_origin (src2);

  dst = cvCreateImage (cvGetSize (src1), IPL_DEPTH_8U, 1);

  superpose (src1, src2, dst);

  cvNamedWindow (window_title, CV_WINDOW_AUTOSIZE);
  cvShowImage (window_title, dst);
  cvWaitKey(0);
  cvDestroyAllWindows();

  cvReleaseImage(&src1);
  cvReleaseImage(&src2);
  cvReleaseImage(&dst);

  return EXIT_SUCCESS;
}

However, it is interesting to note that this kind of function already exists in OpenCV, with cvAddWeighted :

void superpose (const IplImage *src1, const IplImage *src2, IplImage* dst)
{
  cvAddWeighted (src1, 0.5, src2, 0.5, 0.0, dst);
}

Blow ! This chapter was dense. Very dense, even.

I highly recommend you read it again when you have digested the Paracetamol that you just swallow. The notions that we have just seen, are fundamental for the future !

Also, you can be reassured : if you have correctly assimilated what we have come to see, the rest of this course, you will surely much more easy.