“This dream bleuuuuu… ”
Ah ! Are you there ?… Hum !… Hello ! I didn’t have you seen…

You’ve probably guessed it : today, we’re going to talk about colors.

In the previous chapter, we discovered all the images in the simplest case : that of grayscale images. However, we know very well, you and me, that unless you have the blues or to suffer a very serious form of color blindness, the world we see is not gray but colorful.

To correct this, we will now refine our representation of the light of way to bring in the concept of colour (or rather color), and we’ll see how that translates on the digital images. If you have followed what we have discussed up to now, this chapter, should seem much easier than the previous one.

Theoretical representation of the colors

The luminance and chrominance

As I said earlier, the gray levels in an image representing a light intensity at each pixel. They are said to describe the luminance, that is to say, theinformation related to the intensity of the light. This is to consider light as a carrier of a single piece of information, describable by a single number : the level of gray. If we think in terms of light waves, we can consider, roughly speaking, that this information is translated by the’amplitude of the wave.

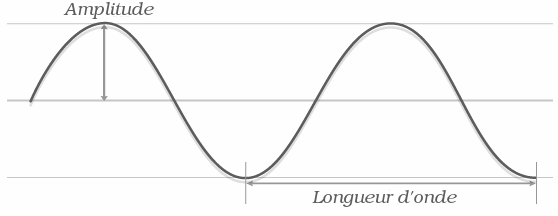
Only, in the real world, the light is not reduced in its intensity, just as a wave cannot be described not only by its amplitude but also by its frequency (or its wavelength, but the two are measures of the same information). You probably know that the frequency of a light wave affects the color we perceive when the ray hits our retina : from red to violet through all the shades of the rainbow. This second information carried by the light, we call it the chroma.

It is in this that a color image will differ from grayscale images : each pixel will be a carrier rather than a single piece of information (the luminance), but two (luminance and chrominance).
In practice, you will understand that to contain several different information, the pixels must be composed of multiple numbers… in other words, images must be composed of multiple channels.

The color spaces

Contrary to what you have to think and although we now consider the light as a carrier of both, we’re not going to work with pixels composed of two numbers but three. This is due to the fact that the light rays are a little bit more complex in reality, simple waves, and that a single dimension is not sufficient to describe effectively the information of chroma, in particular.

Mathematically speaking, this amounts to consider that our pixels are vectors in a three-dimensional space. In fact, there are several ways to encode the color on three numbers, and each of these ways of defining the color describes a color space that is different. Given that we are about to begin, we will start by working in a single space for the moment, but you will have the opportunity to discover several other in this tutorial, each with its own way of coding the colors, its history, its qualities and its defects.

Read similar articles from  the eyesweb project

The space RGB

To make the connection between the physical light and the model RGB, let’s imagine that we make a small optical experiment.

As you may know, white light is the result of the superposition of waves of all frequencies visible in a same radius. Let’s imagine that we pass a ray of white light through a filter absorbing the blue (that is to say that we will remove all the high-frequency range of light), we would obtain then a yellow ray. If, now, we can remove all the light waves of low frequency of the yellow ray, through a filter that absorbs the red, we would get a ray green.

What can we learn from this experience ?
Just that the color of the light can be seen as a careful balance of three basic components : red (red, R), green (green, G), and blue (blue, B). We have described the principle of theRGB colour space.

The principle of the superposition of the color space RGB.

Mathematically speaking, we will represent a color space RGB by a vector $(r,g,b)$containing the levels of red, green, and blue corresponding. Given that we are working for the moment on numbers taking on a byte, these values, in a manner similar to grayscale, will be between 0 and 255.

For example, one can associate the following colors to their representations in the space-to RGB :

RGB and the luminance

Although the space RGB is used extensively in computer science (it is even the most used), it is characterized by a fairly large defect that it is a good idea to raise now : in this space, the luminance information and chrominance are intertwined it is to say that one will not find, for example, the information of full luminance on one channel and the chrominance on the other two. In computer vision, it happens that this is a real problem, for example when one is trying to create an algorithm independent of variations in brightness (which sometimes involves work only on the chroma, as we will see when we discuss, much later, the segmentation color).

Rather than immediately respond to this problem by introducing a new color space (which is not relevant at this level of the tutorial), I think the most important thing is to show you how to extract the luminance information of a pixel encoded in space RGB. In other words, how to juggle between the RGB and grayscale.

To move from one level of grey to its value in the space RGB, the conversion is obvious. If $p_{\mathrm{gris}} = y$, then its equivalent will be $p_{\mathrm{RGB}} = (y,y,y)$ : you can simply replicate the level of gray on the channels red, green and blue to get the same tone.

For the transition in reverse, on the other hand, it is a little more complicated. One might think, a little naively, that the gray level is simply the average of the levels of red, green, and blue of a given color. Although this is an acceptable approximation of the luminance, it is also to overlook the fact that the frequency ranges corresponding to the colours red, green, and blue light do not occupy the same place on the visible spectrum, so that the three components do not contribute all in the same way to the brightness. In fact, the green component contributes more to the luminance than the other two. Thus, to take into account during the extraction of the luminance, one assigns weights to the RGB components. The classic formula of conversion is :

$p_{\mathrm{gris}} = 0.299 \times r + 0.587 \times g + 0.114 \times b$

In practice, of course, you don’t need to know this formula by heart, since OpenCV will apply it for you, as we will see later.

Working with color images

Data representation

As I suggested at the beginning of the chapter, the pictures in colour differ from those in gray levels by the fact that they are composed of several channels. To put it simply, an image in RGB will be composed of three channels : a red channel, a green channel and a blue channel. This information is accessible on the structure IplImage thanks to its field nChannels.

Decomposition of the channels red, green, and blue Lena (click on the images to enlarge them).
Note that in 1973, the scanner blue of the IIPS was of poor quality…
Another amusing detail : the JPEG compression of thumbnails takes obviously into account the weight of the RGB components in the luminance…

In reality, this history channel doesn’t really reflect what happens in memory : the image in question will not be made up of three arrays of the same dimensions, but of one whose pixels take three times more space. It is said that the channels are interleaved. Another important thing to know is that in OpenCV, the color-space by default is not RGB, but BGR. The second differs from the first simply by the fact that the blue channel and red channel are swapped. The following diagram summarizes the situation :

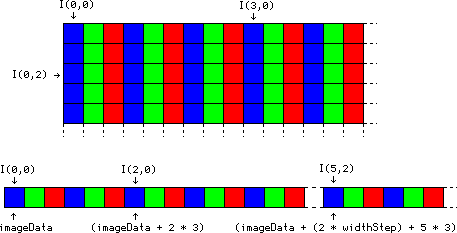
If you remember the diagram of the previous chapter on images in the grayscale, you will find that the only thing that’s changing, finally, when one wants to access the address of a given pixel, it is that it is necessary to multiply its coordinate $x$ by 3.

In the end, to work in colour at a low level, it is simply to take account of the fact that if we think in terms of char* on an image BGR 8-bit :

• (img->imageData + (2 * img->widthStep) + 12 * 3) is the address of the blue component of the pixel coordinate $(12,2)$,

• (img->imageData + (2 * img->widthStep) + 12 * 3 + 1) is the address of the green component of this pixel,

• (img->imageData + (2 * img->widthStep) + 12 * 3 + 2) is the address of its red component.

Now that this is installed, find out the two possible ways of dealing with the processing of color images.

The approach ” one pixel = one color

The first way of dealing with images in multi-channel in OpenCV is to continue to look at the image as a matrix whose pixels are vectors. To do this, and this, with the simple goal of making echo in the previous chapter, we may introduce new features to OpenCV, which let you retrieve and change the values of the pixels as well as the structure CvScalarthat represents a pixel in a color image.

typedef struct CvScalar
{
    double val[4];
}
CvScalar;

As you can see, this structure could not have been more simple. If it can hold up to four values, this is simply because that OpenCV supports images, which can have up to 4 channels, while the fourth channel is used almost never in practice.

To create a scalar you can use the following manufacturers :

/* Construit un CvScalar en utilisant les quatre valeurs indiquées */
CvScalar cvScalar (double val0, double val1, double val2, double val3);

/* Construit un CvScalar en initialisant les quatre valeurs à val0123 */
CvScalar cvScalarAll (double val0123);

/* Construit un CvScalar en initialisant val[0] à val0, et les trois autres valeurs à 0 */
CvScalar cvRealScalar (double val0);

Or, more semantic, and probably more direct in many cases, the following macro :

#define CV_RGB( r, g, b )  cvScalar( (b), (g), (r), 0 )

To interact with an image in the middle of this structure, you can use the following two functions :

/**
 * Récupère le pixel de coordonnées (idx1, idx0) sous forme d'un CvScalar
 */
CvScalar cvGet2D (const CvArr* arr, int idx0, int idx1);

/**
 * Remplace le pixel de coordonnées (idx1, idx0) par 'value'
 */
void cvSet2D (CvArr* arr, int idx0, int idx1, CvScalar value);

As for the function cvPtr2D (that it is possible to use also), these functions take the first argument is the y coordinate, then the x coordinate of the pixel in question.

Example

As an example of how to use these functions, here is a function invert_color that inverts a color image.

void invert_color (IplImage* img)
{
  CvScalar p;
  int x, y, k;

  assert (img->depth == IPL_DEPTH_8U);

  for (y = 0; y < img->height; ++y)
  {
    for (x = 0; x < img->width; ++x)
    {
      p = cvGet2D (img, y, x);
      for (k = 0; k < img->nChannels; ++k)
      {
        p.val[k] = 255 - p.val[k];
      }
      cvSet2D (img, y, x, p);
    }
  }
}

This approach is relatively simple, even if the compulsory passage through the structure CvScalar is rather verbose, and mostly quite slow compared to direct access to pointers, in particular because this function performs in-house casts, copies, and verifications in every sense.

Now here is the same function implemented this time in a direct way and more effective.

void invert_color (IplImage* img)
{
  uchar *p, *line;

  assert (img->depth == IPL_DEPTH_8U);

  for (line =  (uchar*) img->imageData;
       line <  (uchar*) img->imageData + img->imageSize;
       line += img->widthStep)
  {
    for (p = line; p < line + img->width * img->nChannels; ++p)
    {
      *p = 255 - *p;   
    }
  }
}

As you can see, this function differs very, very little of what we saw in the previous chapter. The only thing that has been added, it is the multiplication of the number of columns of the image by its number of channels to go through the whole line. Once again, I recommend you to favour this kind of method compared to the use of the functions of the API of OpenCV to access the pixels of your images.The fact of not having to make the calls to the functions from a library at each iteration to interact with the data is a definite advantage from the point of view of performance.

So that it remains clear in your mind, keep this little classification in mind in regards to the methods to access the pixels :

cvGet2D < cvPtr2D < direct access

Here are the result of the two previous functions on Lena :

The approach of ” Divide and conquer “

Well, first of all, the previous approaches are those that seem the most logical to process images in color, they may be sometimes insufficient or inappropriate to generalize some treatments on the grey levels of the images in color (for example, filtering, or equalization of histograms, as you will soon see). In fact, sometimes it is necessary to process each channel of the image independently of the other two. For this, we will need to separatethe three channels into three different images (split), apply the treatments on each channel, and then reconstruct the three channels into a single image (merge).

For this, OpenCV offers us the following two functions :

/**
 * Sépare une image multi-canaux en plusieurs images à un seul canal.
 * Arguments :
 * - src : image à séparer
 * - dst0, dst1, dst2, dst3: images dans lesquels placer les canaux
 */
void cvSplit (const CvArr* src, CvArr* dst0, CvArr* dst1, CvArr* dst2, CvArr* dst3);

/**
 * Fusionne plusieurs images à un seul canal en une image multi-canaux.
 */
void cvMerge (const CvArr* src0, const CvArr* src1, const CvArr* src2, const CvArr* src3, CvArr* dst);

In both functions, the arguments are not used (classically dst3 and src3 most of the time) will be left NULL.

In order to illustrate the use of these functions, here is a final implementation of the function invert_color :

void invert_color (IplImage* img)
{
  IplImage* chans[3];
  int i = 0;

  assert (img->nChannels == 3);
  assert (img->depth == IPL_DEPTH_8U);

  for (i = 0; i < 3; ++i)
  {
    chans[i] = cvCreateImage (cvGetSize (img), IPL_DEPTH_8U, 1);
  }

  // Séparation des canaux
  cvSplit (img, chans[0], chans[1], chans[2], NULL);

  for (i = 0; i < 3; ++i)
  {
    // utilisation de la fonction invert du chapitre précédent
    invert (chans[i]);
  }

  // Refonte des canaux
  cvMerge (chans[0], chans[1], chans[2], NULL, img);

  // Libération des trois images de travail
  for (i = 0; i < 3; ++i)
  {
    cvReleaseImage(chans + i);
  }
}

This function is a little more complicated than the previous. On the other hand, it illustrates an advantage non-negligible in the method “split & merge ” : if you have access to a given function handling a single channel, this is how you can apply it to color images without having to know the ins and outs. Of course, the use of this approach makes even more sense when treatments applied on the three channels are not the same…

A final function for the road

Before moving on to the exercises in this chapter, I have one last feature to show you, and not the least ! See for yourself :

/**
 * Conversion entre deux espaces de couleur.
 * arguments:
 * - src, dst: images source et destination de la conversion
 * - code: code décrivant l'algorithme de conversion à utiliser
 */
void cvCvtColor(const CvArr* src, CvArr* dst, int code);

The argument code is managed by the constants of OpenCV that take the form :
CV_[espace de départ]2[espace d'arrivée].

For example, to convert an image to BGR in grey levels, the code will be CV_BGR2GRAY, and the inverse transformation is CV_GRAY2BGR. The documentation of this functiondescribes the formulas used to perform the conversions of the most common.

Exercises

Reinvention of the wheel

Although this exercise will make you do anything spectacular, I find that the best way to make you “feel” the images in color is still you to manipulate in reinventing the wheel, that is to say, by re-implementing the functions cvSplit and cvMerge.

Explore more topics from the eyesweb system

The aim of the exercise is to make you code the small program that I used to show you the decomposition into channels of Lena a little earlier in the chapter. To do this, you will first need to encode the following functions :

/**
 * Sépare les canaux d'une image BGR 8 bits en trois images mono-canal 8 bits.
 */
void my_split (const IplImage* src, IplImage* blue, IplImage* green, IplImage* red);

/**
 * Assemble une image BGR 8 bits à partir de trois images mono-canal 8 bits.
 */
void my_merge (const IplImage* blue, const IplImage* green, const IplImage* red, IplImage* dst);

I highly recommend the use of the function cvPtr2D to browse the images inside of these functions.

Then, you can use these functions in a program that will disassemble a color image, and reassemble three new images corresponding to the channels red, green, and blue of the original image, that is to say that for the blue channel, for example, you will need to provide my_merge an image 8-bit single-channel black for the channels green and red (the function cvSetZero should be useful.)

Correction

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <opencv/cv.h>
#include <opencv/highgui.h>

/**
 * Sépare les canaux d'une image BGR 8 bits en trois images mono-canal 8 bits.
 */
void my_split (const IplImage* src, IplImage* blue, IplImage* green, IplImage* red)
{
  int x,y;
  uchar *p_src, *p_red, *p_green, *p_blue;

  for (y = 0; y < src->height; ++y)
  {
    for (x = 0; x < src->width; ++x)
    {
      p_src   = cvPtr2D (src,   y, x, NULL);
      p_blue  = cvPtr2D (blue,  y, x, NULL);
      p_green = cvPtr2D (green, y, x, NULL);
      p_red   = cvPtr2D (red,   y, x, NULL);

      *p_blue  = *p_src;
      *p_green = *(p_src + 1);
      *p_red   = *(p_src + 2);
    }
  }
}

/**
 * Assemble une image BGR 8 bits à partir de trois images mono-canal 8 bits.
 */
void my_merge (const IplImage* blue, const IplImage* green, const IplImage* red, IplImage* dst)
{
  int x,y;
  uchar *p_dst, *p_red, *p_green, *p_blue;

  for (y = 0; y < dst->height; ++y)
  {
    for (x = 0; x < dst->width; ++x)
    {
      p_dst   = cvPtr2D (dst,   y, x, NULL);
      p_blue  = cvPtr2D (blue,  y, x, NULL);
      p_green = cvPtr2D (green, y, x, NULL);
      p_red   = cvPtr2D (red,   y, x, NULL);

      *p_dst       = *p_blue;
      *(p_dst + 1) = *p_green;
      *(p_dst + 2) = *p_red;
    }
  }
}

/** 
 * usage: IMG B G R
 * - IMG: image dont les canaux sont à séparer
 * - B:   sortie du canal bleu
 * - G:           "       vert
 * - R:           "       rouge
 */
int main (int argc, char* argv[])
{
  int i;

  const char* rgb_path;
  const char* c_path[3];

  IplImage* rgb;
  IplImage* black;
  IplImage* chans[3];
  IplImage* tmp;

  if (argc != 5)
  {
    fprintf(stderr, "usage: %s IMG B G R\n", argv[0]);
    return EXIT_FAILURE;
  }

  rgb_path = argv[1];

  if (!(rgb = cvLoadImage (rgb_path, CV_LOAD_IMAGE_COLOR)))
  {
    fprintf (stderr, "couldn't open image file: %s\n", rgb_path);
    return EXIT_FAILURE;
  }
  
  /* Initialisation des images de travail */
  black = cvCreateImage (cvGetSize (rgb), IPL_DEPTH_8U, 1);
  tmp = cvCreateImage (cvGetSize (rgb), IPL_DEPTH_8U, 3);
  cvSetZero (black);

  for (i = 0; i < 3; ++i)
  {
    c_path[i] = argv[2+i];
    chans[i] = cvCreateImage (cvGetSize (rgb), rgb->depth, 1); 
  }

  /* Séparation des canaux */
  my_split (rgb, chans[0], chans[1], chans[2]);

  /* Reconstruction dans des images couleur */
  my_merge     (chans[0], black, black, tmp);
  cvSaveImage (c_path[0], tmp, NULL);
  my_merge     (black, chans[1], black, tmp);
  cvSaveImage (c_path[1], tmp, NULL);
  my_merge     (black, black, chans[2], tmp);
  cvSaveImage (c_path[2], tmp, NULL);

  /* Libération de la mémoire */
  for (i = 0; i < 3; ++i)
  {
    cvReleaseImage (chans + i);
  }
  cvReleaseImage (&black);
  cvReleaseImage (&tmp);
  cvReleaseImage (&rgb);

  return EXIT_SUCCESS;
}

We have now finished with the basic notions on the images. Now that you know how to work with, either in math or in your programs, you can begin to read the parts of this course related to image processing.

This part is not finished yet. Other chapters will enrich as. Nevertheless, with the chapters that are already present, you can already follow the continuation of this course.